O Que É um Histograma
O histograma, também conhecido como diagrama de barras ou diagrama de frequência, além de ser um método estatístico para análise de dados, também faz parte das 7 ferramentas da qualidade.
Ele consiste na representação gráfica de colunas (retângulos), onde é apresentado uma distribuição de frequências afim de visualizar, de maneira rápida, a variabilidade dos dados coletados. Ou seja, mede quantas vezes um conjunto de valores aparece em uma amostra de informações.
Nesse sentido, a configuração do método permite que, pelo resultado obtido, tire-se uma conclusão imediata da dispersão do grupo de valores da distribuição.
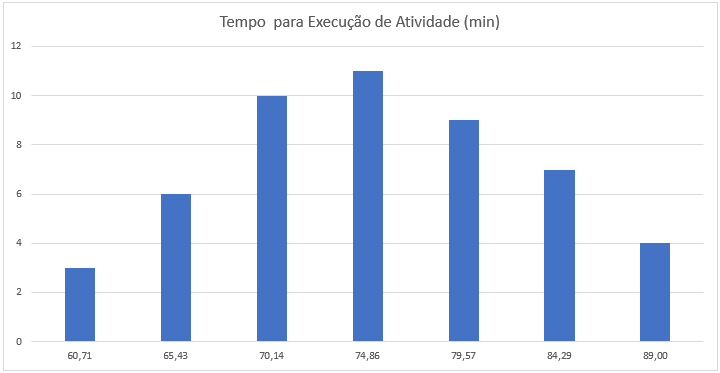
Na exibição gráfica, cada base de coluna representa uma classe de dados com limites (range de valores) pré-estabelecidos, já a sua altura representa a quantidade dos fatores ou ocorrências das grandezas analisadas.
A utilização dos gráficos de barras verticais para explicar fenômenos existe antes mesmo do surgimento dos histogramas, por volta do século XVIII. Porém, a técnica era restrita aos estudos relacionados ao comércio internacional e mortalidade em guerras civis.
O primeiro uso do histograma foi realizado pelo advogado francês André Michel Guerry, em 1883. Assim, o método foi utilizado para analisar a criminalidade contra a população em Paris.
Tipos de Histogramas
De modo geral, os tipos de histogramas podem variar de acordo com dois fatores: centralidade e dispersão.
Denomina-se um diagrama de centralidade quando as frequências de valores tendem a ser maiores nas colunas do meio. Já a dispersão está relacionada com a variabilidade dos valores. Ou seja, o número de colunas.
Dessa forma, o diagrama pode ter tendência central ou não central. Além disso, também podem possuir alta ou baixa dispersão. De modo geral, os tipos são:
- Tendência central
- Multimodal
- Tendência assimétrica negativa
- Tendência assimétrica positiva
- Duplo pico
- Achatado

Utilização do Histograma
Analisar dados pode ser uma tarefa extremamente complexa, dependendo da quantidade de informações que se tem. Com isso, a aplicação do histograma recebe abrangência da indústria à medicina.
Nesse sentido, o uso da ferramenta é amplamente aceito quando o volume de dados para se examinar tem uma quantidade considerável. Pois, após a elaboração do gráfico a visualização da frequência torna-se imediata.
Assim, algumas aplicações do histograma são, por exemplo:
- Análise de dados financeiros
- Identificação de desvios em processos produtivos
- Verificação de problemas
- Observação de tendências em padrões de doenças
- Identificação no aumento da obesidade em populações
Como Fazer um Histograma
Existem algumas ferramentas que pode auxiliar durante a construção do gráfico, como por exemplo: MS Excel, Minitab, Pictovia, Tableau, etc. Para este exemplo, iremos utilizar o MS Excel.
Assim, antes de iniciar a elaboração do histograma, torna-se essencial o entendimento de alguns elementos importantes para a elaboração técnica do gráfico. Estes são:
- Amostra: subconjunto retirado de um conjunto de informações.
- Valor Mínimo: menor valor da amostra.
- Valor Máximo: maior valor da amostra.
- Amplitude: diferença entre Valor Máximo e o Valor Mínimo.
- Classe: agrupamento de dados da amostra, também corresponde ao número de barras do histograma.
- Frequência: número de valores em cada classe.
Agora, basta seguir os passos citados abaixo e elaborar o seu próprio diagrama de frequência.
1. Coletar as informações:
Antes de iniciar a elaboração do histograma, reúna os dados da amostra da qual se deseja analisar.
2. Organizar os dados:
Formate as informações em uma tabela.
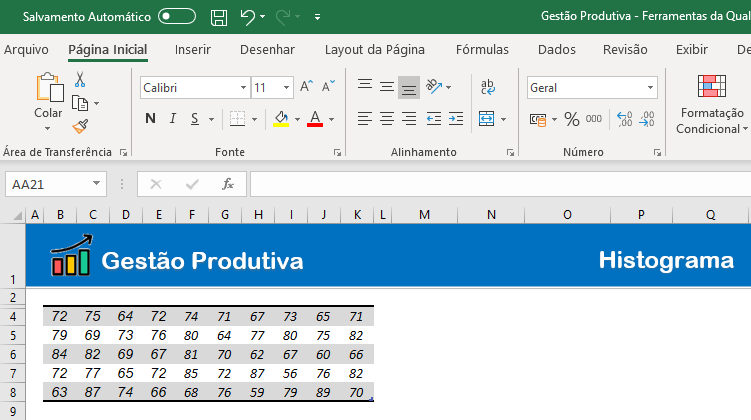
3. Criar uma tabela auxiliar para as demais informações:
Nesse passo, pode-se começar pela quantidade de elementos da amostra.
Então, utilize a fórmula “=CONT.NÚM” e selecione a tabela para obter o número de elementos da amostra.
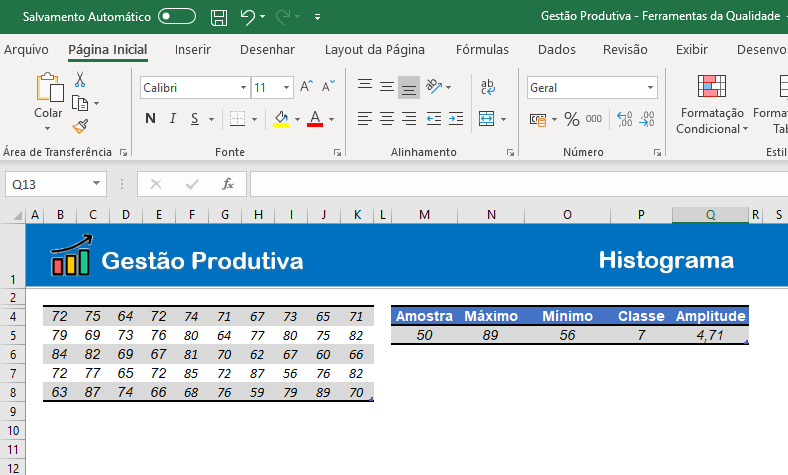
4. Descobrir os valores de Máximo e Mínimo do conjunto.
Para isso, use a fórmula “=MÁXIMO” e “=MÍNIMO” para facilitar a exibição dos valores.
5. Determinar a Classe:
Determine o número de classes calculando a raiz da amostra. Neste caso, como a raiz não é um valor inteiro incremente a fórmula com “INT”. Assim, ficará da seguinte forma: “=INT(RAIZ”.
6. Estabelecer a Amplitude da amostra:
Calcule a amplitude da seguinte maneira: “(MÁXIMO – MÍNIMO) / NÚMERO DE CLASSES
7. Calcular os limites de frequência:
Estabeleça o primeiro limite da primeira classe somando o “MÍNIMO + AMPLITUDE”. Após, os demais limites serão obtidos somando o “VALOR ANTERIOR + AMPLITUDE.”
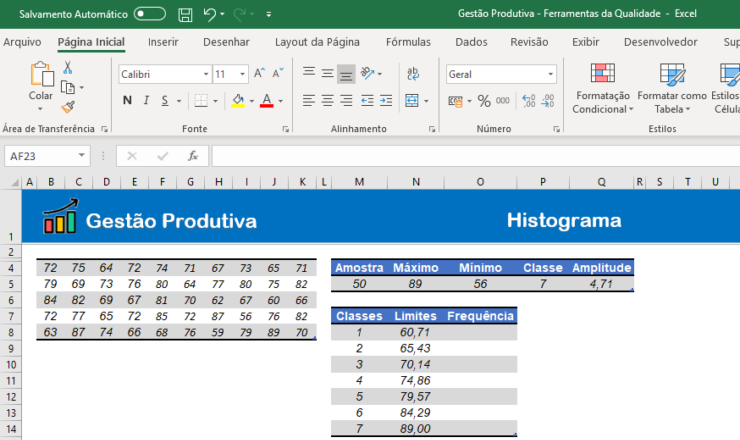
8. Calcular a frequência dos elementos:
Utilize a fórmula =CONT.SES(TABELA;”<=”&PRIMEIRO LIMITE) para calcular a primeira frequência.
Após, use a fórmula =CONT.SES(TABELA;”>”&PRIMEIRO LIMITE;TABELA;”<=”&SEGUNDO LIMITE) para a segunda frequência e arraste a fórmula para baixo, concluindo todos os valores restantes.
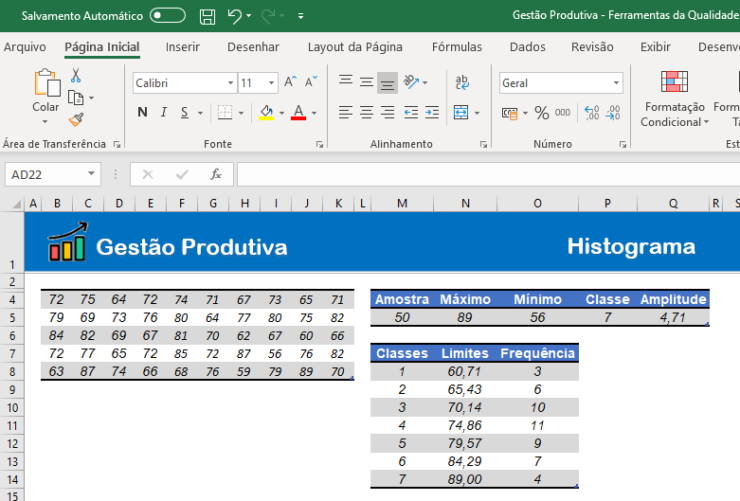
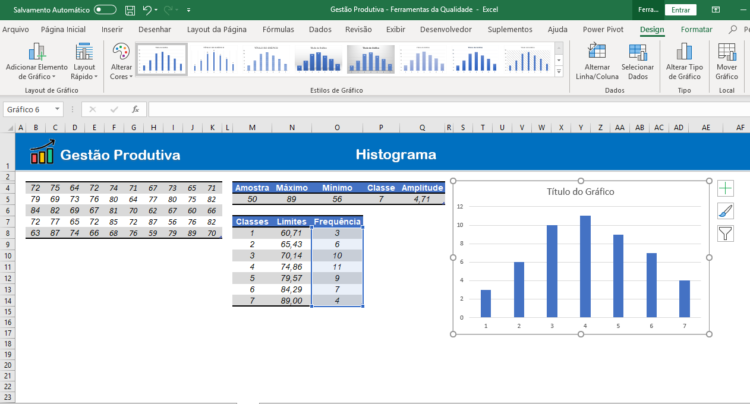
9. Plotar o gráfico de colunas:
Selecione a colune de “Frequência” e insira um gráfico de colunas 2D. Após, configura as demais informações, como por exemplo: título, largura, altura, eixo de série, etc.
Fatores Importantes no Uso do Histograma
Durante a aplicação do histograma existem alguns fatores imprescindíveis para facilitar a análise visual dos dados coletados da amostra.
Para assim, facilitar a tomada de decisão com base a frequência das informações, como por exemplo:
- Adequar o número de classes para no mínimo 7.
- Configurar a largura das colunas para melhor visualização do gráfico.
- Manter uma amplitude igual para facilitar a interpretação
- Utilizar um gráfico de controle para auxiliar na tomada de decisão
- Utilizar o limite inferior da primeira frequência menor ou igual ao menor dos valores da amostra
- Usar apenas uma classe para cada valor
Portanto, analisar dados pode ser uma tarefa extremamente complexa, nota-se a dificuldade principalmente quando o volume de informações é grande. Para isso, o histograma é um grande suporte na realização desta tarefa.